There are two ways to calculate the attention in transformer: one is $\text{Attention(Q, K, V)}=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\times V$ same as in Attention Is All You Need, the other is $\text{Attention(Q, K, V)}=V \times\text{softmax}(\frac{K^TQ}{\sqrt{d_k}})$ from here. Depending on different context, both are correct. The key point is How You Organize the Input.

I manage to go over the vector version of the attention and then derive the matrix form.

Vector Version

The aim of the attention mechanism is to map a query and a set of key-value pairs to an output.

Suppose we have sets of vectors: input $x$, query, key, and value with dimensions $d_p$, $d_q$, $d_k$, and $d_v$ respectively, where $d_q = d_k$ For each input $x_i$, there are corresponding $q_i$, $k_i$, and $v_i$.

Denote

$$
a_{1, i} = \frac{q_1 \cdot k_i}{\sqrt{d_k}} \text{, where }i=1, 2, \dots
$$

What $a_{1, i}$ means is a vector of products between the input $x_1$ and other keys. The name, scaled dot-product, is from dividing $\sqrt{d_k}$. It’s introduced to tackle the problem made by magnitude in computation, and also can be checked in the article.

Then, the output 1 is

$$
\begin{align*}
o_1 &= \sum_i \hat{a_{1, i}} \cdot v_i &\text{where } \hat{a_{1, i}} = \text{softmax}(a_{1, i}), i=1, 2, \dots
\end{align*}
$$

The softmax function converts a vector of numbers into a vector of probabilities [wiki], and the outcome 1 is the sum of the scalar multiplications of the scalar $\hat{a_1, i}$ and the vector $v_i$.

Usually, the result of the attention function has the same shape of the input.

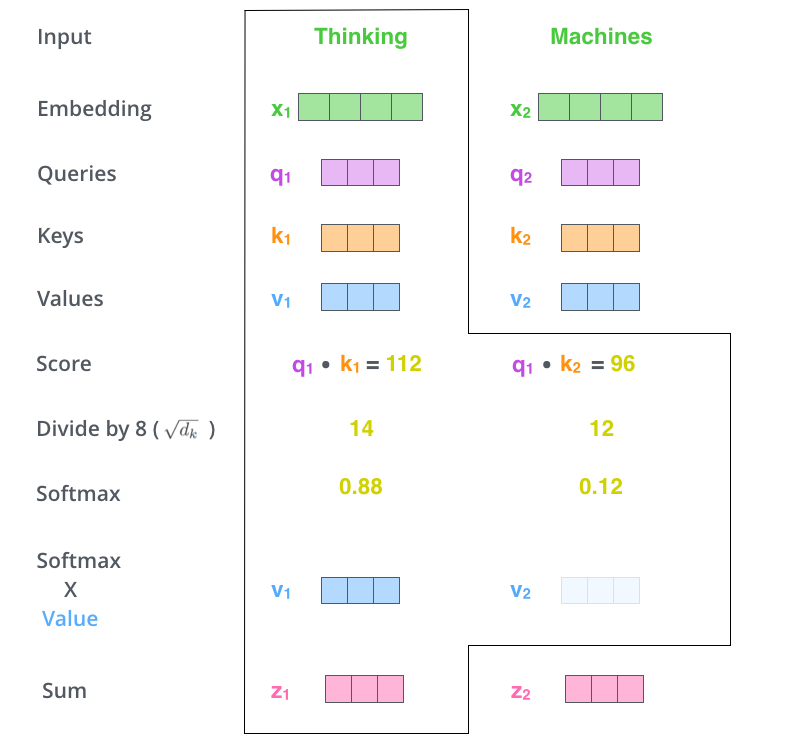
Matrix Version

Different from the vector version, there is one more step before the attention calculation for the matrix version. The query, key and value are not given directly, but they are computed from matrices $W^Q$, $W^k$, and $W^v$.

Suppose we have the input with shape $[n, p]$. The weight matrices are going to be $[p, d_q]$, $[p, d_k]$, and $[p, d_v]$. $n$ is just the number of inputs, or in another words, the batch size.

Then,

$$
Q: [n, d_q]
$$
$$ K: [n, d_k]
$$

$$ V: [n, d_v]
$$

Since each row of Q has to multiply each row in K, we can transpose the K and make a matrix multiplication $Q \cdot K^T$. The result is a $n \times n$ matrix, each row is the result corresponding to the vector version. For example, in the first row there are elements $a_{1, 1}, a_{1, 2}, \dots, a_{1, i},$.

$$
\begin{pmatrix}
\alpha_{1, 1}=q^1\cdot k^1 & \alpha_{1, 2}=q^1\cdot k^2 & \cdots & \alpha_{1, i}=q^1\cdot k^k \\
\vdots & \alpha_{2,2} & \cdots & \vdots \\
\alpha_{n, 1} & \cdots & \cdots & \alpha_{n,i}
\end{pmatrix}
$$

Dividing $\sqrt{d_k}$ and applying softmax function do not change the shape of this $n \times n$ matrix, so we are going to multiply V with a $n \times n$ matrix.

Please pay attention (pun),

$$
\begin{align*}
o_1 &=\sum_{i}\hat{a}_{1,i}v_i \\
&= \hat{a}_{1,1}v_1 + \hat{a}_{1,2}v_2 + \cdots + \hat{a}_{1,i}v_i \\
&= \begin{pmatrix}
v_1 & v_2 & \dots & v_i
\end{pmatrix} \begin{pmatrix}
\hat{a}_{1,1} \\
\hat{a}_{1,2} \\
\vdots \\
\hat{a}_{1,i}
\end{pmatrix} \\
&= \begin{pmatrix}
\hat{a}_{1,1} & \hat{a}_{1,2} & \cdots & \hat{a}_{1,i}
\end{pmatrix}\begin{pmatrix}
v1 \\ v2 \\ \vdots \\ v_i
\end{pmatrix}
\end{align*}
$$

any $\hat{a}$ is a scalar, but any v is a vector.

Therefore, we can have

$$
\begin{align*}
\text{Attention(Q, K, V)}&=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\times V\\
&=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\times \begin{pmatrix}
v1 \\ v2 \\ \vdots \\ v_i
\end{pmatrix}.
\end{align*}
$$

This is exactly what this figure is doing(Adding a mask is optional).

Jay’s figures perfectly express shapes of matrices in calculation.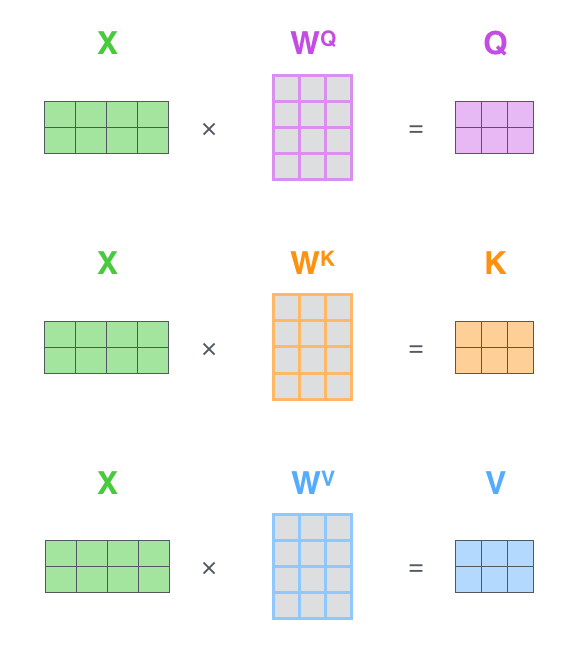

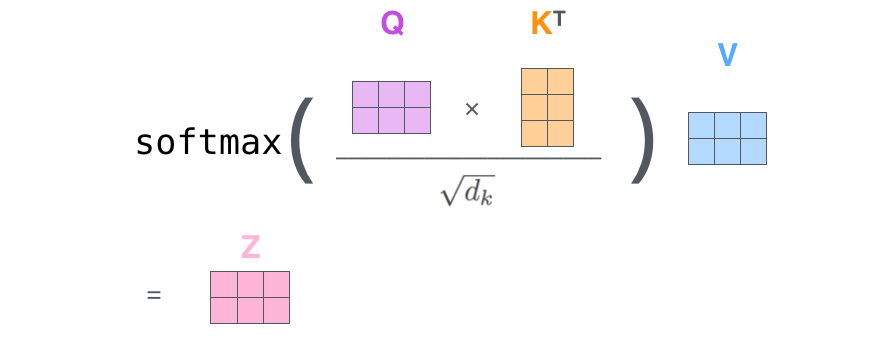
the other Formula

However, the matrix multiplication isn’t invertable like scalar multipication. The formula above cannot give the anticipant results, if we cancate vectors of inputs colomn by column into a matrix. In this situation, we have to also transpose the Q, K, V matrices and use the second formula.

$$
\text{Attention(Q, K, V)}=V \times\text{softmax}(\frac{K^TQ}{\sqrt{d_k}})
$$

Conclusion

Understanding the vector version can help to choose the right formula. Most of the case, we use $\text{Attention(Q, K, V)}=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\times V$, such as in PyTorch. But be careful, if the input is a $[p, n]$ matrix.

Code

def compute_QKV(embedding: torch.Tensor,
                Wq: torch.Tensor,
                Wk: torch.Tensor,
                Wv: torch.Tensor) -> typing.Tuple:
    """
    compute Q, V, K matrices by embedding and weights
    :param embedding: shape [n, p]
    :param Wq: shape [p, d_k]
    :param Wv: shape [p, d_v]
    :param Wk: shape [p, d_k]
    :return: Tuple[Q, V, K]
    where Q: shape [n, d_k]
    where K: shape [n, d_k]
    where V: shape [n, d_v]
    """
    return torch.matmul(embedding, Wq), torch.matmul(embedding, Wk), torch.matmul(embedding, Wv)

def scaled_dot_product(Q: torch.Tensor,
                       K: torch.Tensor) -> torch.Tensor:
    """

    :param Q: shape [n, d_k]
    :param K: shape [n, d_k]
    :return: Tensor shape [n, n]
    """
    dk = K.shape[1]
    return torch.matmul(Q, K.T) / torch.sqrt(torch.tensor(dk))

def attention(A: torch.Tensor,
              V: torch.Tensor) -> torch.Tensor:
    """

    :param A: shape [n, n]
    :param V: shape [n, d_v]
    :return: Tensor with shape [n, d_v]
    """
    A_prime = torch.softmax(A, dim=1)
    assert 0.9 < A_prime[0].sum() < 1.1   # do softmax row by row
    return torch.matmul(A_prime, V)

Example

Done by the first approach

$$
\text{Attention(Q, K, V)}=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\times V
$$

embeddings = torch.tensor([
    [1, 1, 1, 0],
    [1, 2, 1, 0],
    [0, 1, 0, 1],
    [0, 1, 1, 0]
])
Wq = torch.tensor([
    [1, 0, 1],
    [1, 1, 1],
    [0, 0, 1],
    [1, 0, 0]
])
Wk = torch.tensor([
    [1, 0, 0],
    [1, 1, 1],
    [1, 0, 1],
    [0, 1, 0]
])
Wv = torch.tensor([
    [1, 2, 0],
    [1, 3, 1],
    [1, 0, 2],
    [1, 1, 0]
])

Q, K, V = compute_QKV(embeddings, Wq, Wk, Wv)


A = scaled_dot_product(Q, K)


Aprime = torch.softmax(A, dim=1)
torch.matmul(Aprime, V.type(torch.float))

tensor([[3.9492, 7.8588, 3.9577],
        [3.9924, 7.9784, 3.9934],
        [3.8407, 7.5669, 3.8595],
        [3.7902, 7.4482, 3.8228]])

1	attention(A.type(torch.float), V.type(torch.float))

tensor([[3.9492, 7.8588, 3.9577],
        [3.9924, 7.9784, 3.9934],
        [3.8407, 7.5669, 3.8595],
        [3.7902, 7.4482, 3.8228]])

Done by the second approach